Dynamic Programming, 하나의 복잡한 문제를 여러 개의 문제로 나누어 해결하는 방법
실행 시간을 줄이기 위해 같은 연산은 반복하지 않고 작은 결과를 바탕으로 규칙을 찾아 점차 큰 결과를 찾는 방법이다.
특징
동적 계획법은 재귀와 유사하다는 생각을 많이 하게 된다.
하지만 재귀 방식은 작은 연산을 반복한다. 그래서 같은 정답 결과를 여러번 연산으로 반복해서 다시 도출하기 때문에 비효율적이다.
그리고 큰 문제를 해결하기 위해서 작게 쪼개서 문제를 해결하는 분할 정복과 비슷하다.
하지만 이 또한 반복을 처리하는 과정에서 중복 여부를 처리하는 과정에서 차이가 있다.
이 차이점을 알아야 dp유형의 문제를 풀 때 보다 확고한 생각을 가지고 문제를 해결하려고 할 수 있다. dp 와의 차이를 꼭 인지해 두자.
dp에서 가장 중요한 특징은 메모이제이션이다.
메모이제이션 : 한번 계산한 문제는 다시 계산하지 않고 저장해두며 활용하는 방식
단골 예시는 피보나치를 한번 보자
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, .....
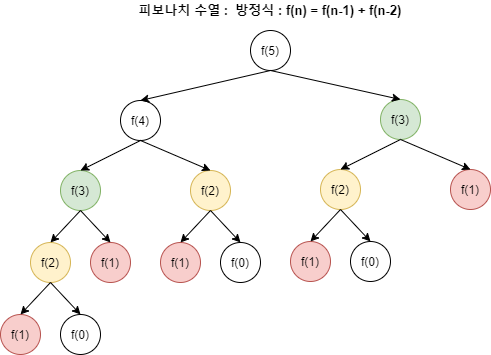
피보나치 수를 구하기 위해선 재귀로 함수를 표현하는 건 워낙 익숙할 것이다.

연산은 위에서부터 아래로 이루어진다. 큰 문제가 풀리지 않아 작은 문제로 세분화 하면서 재귀의 깊이가 깊어지고 있다.이는 StackOverflow가 발생한다. 이처럼 같은 값을 구해도 항상 다시 계산해야 하기 때문에 재귀가 비효율 적이라고 말하는 것이다!
그래서 작은 문제의 결과를 구한 다음, 결과를 기억해 다음 번 연산에서 그 값을 다시 활용하는 것이다.(결과를 재사용)
반복이 없이 연산이 이루어져 연산 횟수가 크게 감소한다.
이는 항상 자주 보던 문제 해결 방식에서 본 두가지 방식과도 관련이 있다.
Bottom-up
작은 문제부터 큰 문제로 차근차근 해결하는 방법, 해결이 용이하지만 가독성이 떨어진다.
Top-down
큰 문제를 풀고 풀리지 않을 경우 작은 문제로 들어가 해결하는 방법 ( 재귀 ), 가독성이 좋지만, 코드를 작성하는 것이 어렵다.
동적 계획법은 bottom-up방식으로 문제를 바라보는 것이 좋다. 그러면서 규칙을 찾아 점화식을 도출하여 문제 해결의 실마리를 얻는 경우가 많다.
DP의 사용 조건
1. Overlapping Subproblems
문제를 나누고 작은 결과를 재사용 해 전체 답을 구하기 때문에 동일한 작은 문제들이 반복해서 나타나는 경우에 사용이 가능하다.
2. Optional Substructure
부분 문제의 최적 결과값을 바탕으로 전체 문제의 최적 결과를 낼 수 있는 경우를 의미한다.
하지만 지겨운 피보나치 예시,, 실제로 풀어보면서 경험해보는 게 낫다고 생각했다.
이제는 배운 내용을 적용해보도록 뒤의 내용을 보자
'Algorithm' 카테고리의 다른 글
| [프로그래머스] Lv.2 튜플 (0) | 2023.02.09 |
|---|---|
| [백준 #1309 파이썬] 동물원 (0) | 2023.01.27 |
| DP 풀이 팁! (0) | 2023.01.06 |
| [백준 #2565 파이썬] 전깃줄 (0) | 2023.01.04 |
| [백준 #2580 파이썬] 스도쿠 (0) | 2023.01.03 |